その6で扱いました、ケーキ店の事例ですが、曜日と明日の天気予報から、明日の販売個数の凡そ予測は、多重クロス表から分かりますが、具体的な予測販売個数はどのように求まるのでしょうか?
それは、重回帰分析を質的データに応用した、数量化Ⅰ類分析で行うことができます。ケーキ店の事例の場合は、具体的には、以下の式の係数を求めることです。
販売予測個数=A0+A1*(日曜/祝日)+A2*(火曜)+A3*(水曜)+A4*(木曜)+A5*(金曜)+A6*(土曜)+A7*(晴)+A8*(曇)+A9*(雨)
ここで、(日曜日/祝日)や(晴)はダミー変数と呼ばれ、0もしくは1の値をとります。該当すれば、1となり、該当しなければ、0となります。
この分析も、Excelの回帰分析で、係数が求められるとともに、重相関係数も得られ、説明力の強さが確認できます。一般に0.8以上が望ましいとされています。
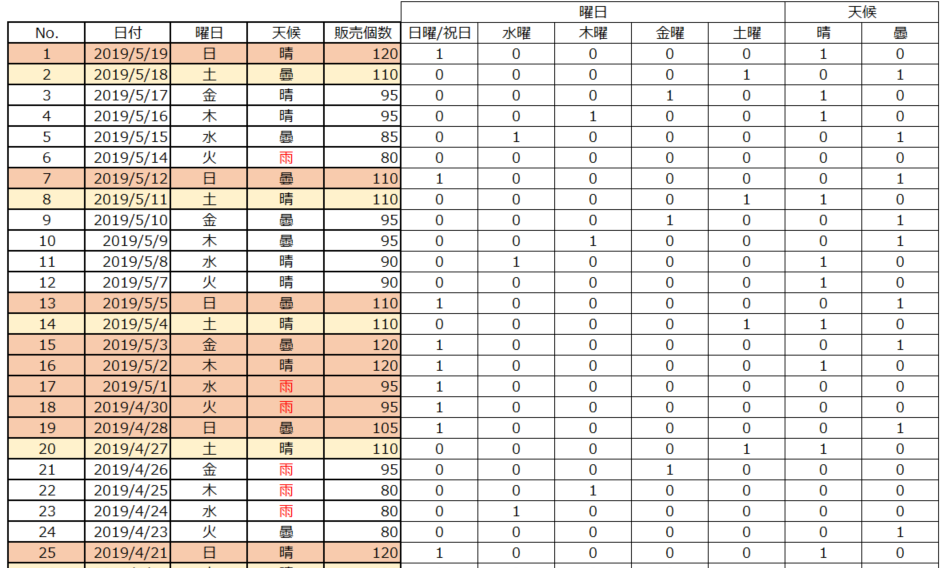
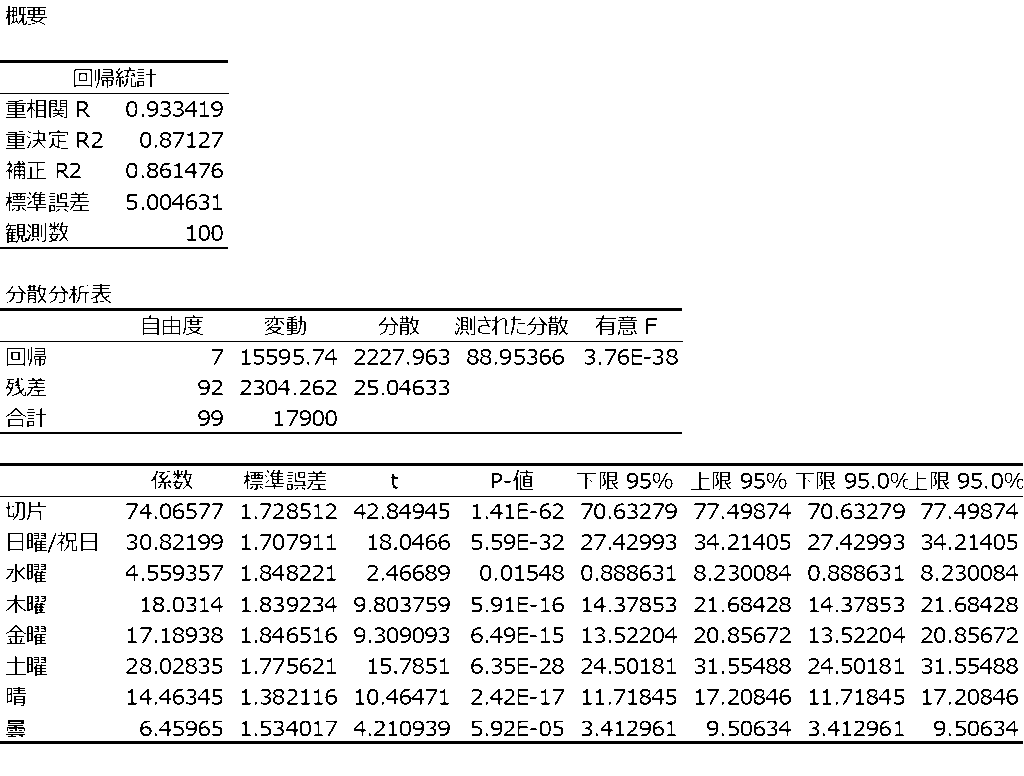
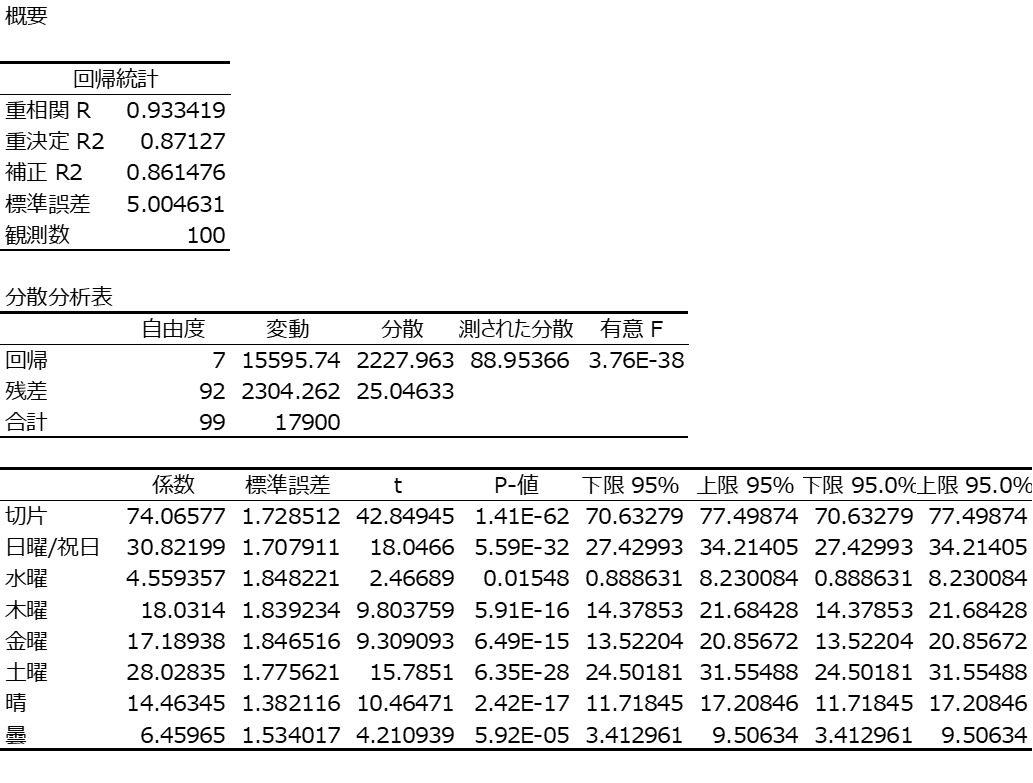
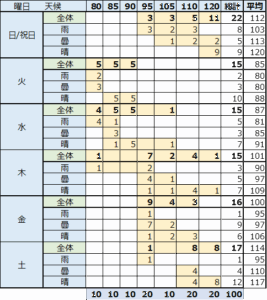
表1に、ダミー変数に変換した100日分のデータの内、直近の25日分のデータを示します。この表に火曜日のダミー変数が無いのは、その他の曜日がすべて0であることで表せるからです。雨が無いのも同じ理由です。このデータを回帰分析することで、図1の分析結果が得られました。
重相関係数は0.93で、十分な説明力と考えられます。求められた、式は以下です。
販売予測個数=74.066+30.822*(日曜/祝日)+0.0*(火曜)+4.559*(水曜)+18.031*(木曜)+17.189*(金曜)+28.028*(土曜)+14.463*(晴)+6.460*(曇)+0.0*(雨)
火曜日と雨の係数が0なのは、その組み合わせの場合の販売個数が定数の74.066個になっているからです。分析結果から、標準誤差が5.0ですから、この式での予測値と実際の販売個数の差の平均は5個と分かります。
このような、販売予測も過去の販売実績データが得られれば、容易にどなたでも、行うことができるとともに、そのモデル式も最新の実績データが増えていくことで、どんどん最新化(モデルの老朽化により、係数を見直す)することもできます。
御社の販売予測を始めてみたいという小売店の皆様、お気軽にご連絡ください。



コメント